Q. At what distance from a convex lens of focal length $30\, cm$, an object should be placed, so that the size of the image be $ \frac{1}{2}th $ of the object?
J & K CETJ & K CET 2004
Solution:
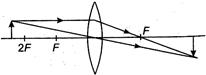
The image formation by a convex lens is as follows:
Image formed is diminished, when object lies between $2 F$ and infinity.
Magnification $(M)=\frac{\text {image size }}{\text { object size}}=\frac{1}{2}=\frac{v}{u}$ ...(i)
From lens formula, $\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$ ...(ii)
where is focal length, $v$ the image distance and $u$ the object distance.
From Eqs. (i) and (ii),
we get $\frac{1}{f}=\frac{1}{u}+\frac{2}{u}$
Given, $u=90\, cm$
$\therefore \frac{1}{30}=\frac{3}{u}$
$\Rightarrow u=90\, cm$