Q.
At time $t=0$, terminal $A$ in the circuit shown in the figure is connected to $B$ by a key and an alternating current $I(t)=$ $I_{0} \cos (\omega t)$, with $I_{0}=1$ A and $\omega=500 \,rad / s$ starts flowing in it with the initial direction shown in the figure. At $t=7 \pi / 6\, \omega$, the key is switched from $B$ to $D$. Now onwards only $A$ and $D$ are connected. A total charge $Q$ flows from the battery to charge the capacitor fully. If $C=20\, \mu F , R=10 \,\Omega$ and the battery is ideal with emf of $50 \,V$, identify the correct statement(s).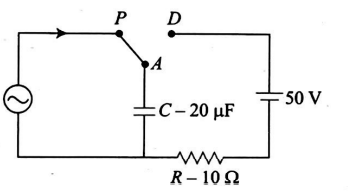
Alternating Current
Solution: