Q. At a random moment within a period of 20 minutes, student 'A' telephones student ' $B$ ', waits for 2 minutes and then puts down the receiver. During the same 20 minutes student ' $B$ ' arrives home at a random moment, stays for 5 minutes and then leaves. Let $P$ denotes the probability that the two will have a talk. If $P=\frac{p}{q}$ as a reduced fraction, then find $(p+q)$.
Probability - Part 2
Solution:


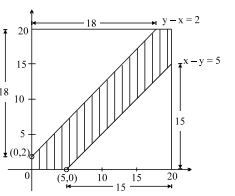
where $0 \leq x \leq 20$ \& $0 \leq y \leq 20$.
Hence $y \leq x+2 \& y \geq x-5$
or
$y - x \leq 2 \& x - y \leq 5 $
$\therefore n ( S )=20 \times 20=400 $
$n ( A )=400-\left[\frac{324+225}{2}\right]$
$ =400-\frac{549}{2}=\frac{251}{2} $
$\therefore p =\frac{251}{2} \frac{1}{400}=\frac{251}{800} \Rightarrow p+q=1051$