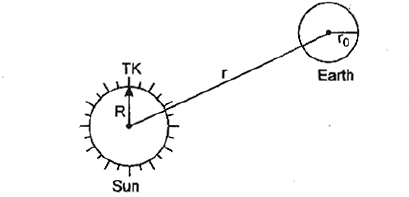
Question

Assuming the sun to be a spherical body of radius R at a temperature of T K, evaluate the total radiant power, incident on earth, at a distance r from the sun :
where $r_{0}$ is the radius of the earth and $\sigma$ is Stefan’s constant.

• A. $4 \pi r_{0}^{2} R^{2} \sigma T^{4} / r^{2}$
• B. $\pi r_{0}^{2} R^{2} \sigma T^{4} / r^{2}$
• C. $r_{0}^{2} R^{2} \sigma T^{4} / 4\pi r^{2} $
• D. $R^{2} \sigma T^{4} / r^{2}$

Answer 1

Answer: (B)

From Stefan’s law, the rate at which energy is radiated by sun at its surface is
$P=\sigma \times4\pi R^{2} \times T^{4}$
[Sun is a perfectly black body as it emits radiations of all wavelengths and so for it e = 1.] The intensity of this power at earth’s surface [under the assumption r > > $r_{0}$] is
$I=\frac{p}{4 \pi r^{2}}=\frac{\sigma\times4\pi R^{2}T^{4}}{4 \pi r^{2}}=\frac{\sigma R^{2} T^{4}}{r^{2}}$
The area of earth which receives this energy is only one half of total surface area of earth, whose projection would be $\pi r_{0}^{2}.$
$\therefore $ Total radiant power as received by earth
$=\pi r_{0}^{2} \times I$
$=\frac{\pi r_{0}^{2}\times\sigma R^{2}T^{4}}{r^{2}}$
$=\frac{\pi r_{0}^{2} R^{2}\sigma T^{4}}{r^{2}}$