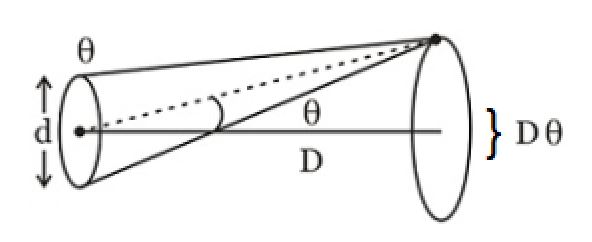
Question

Assuming that the human pupil has a radius of $\text{0.25} \, cm$ and a comfortable viewing distance of $25 \, cm$ . The minimum separation between two point objects that the human eye can resolve for the light of wavelength $500 \, nm$ is

• A. $300 \, μm$
• B. $1 \, μm$
• C. $30 \, μm$
• D. $100 \, μm$

Answer 1

Answer: (C)

By fraunhofer diffraction through a circular aperture, $\theta =\frac{\text{1.22} \lambda }{d}$

d = diameter of pupil $=2\times \text{0.25}=\text{0.5} \, cm$
$\lambda =500 \, nm$
First dark ring is formed by the light diffracted from the hole at an angle $\theta $ with the axis.
Viewing distance, $D=25 \, cm$
$\therefore $ Minimum separation between $2$ objects $=D\theta $
$=\frac{25 \times 10^{- 2} \times 1.22 \times 500 \times 10^{- 9}}{5 \times 10^{- 1}}$
$=30\times 10^{- 6} \, m$
$=30 \, μm$