Q.
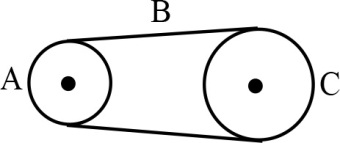
As shown in the figure, wheel $A$ of radius $r_{A}=10 \, cm$ is coupled by a belt $B$ to the wheel $C$ of radius $r_{C}=25 \, cm$ . The angular speed of wheel $A$ is increased from rest at a constant rate of $1.6 \, rad \, s^{- 2}$ . Time after which wheel $C$ reaches a rotational speed of $100 \, rpm$ , assuming the belt does not slip, is nearly
NTA AbhyasNTA Abhyas 2020System of Particles and Rotational Motion
Solution: