Q.
As shown in the figure, two particles, each of mass $'m'$tied at the ends of a light string of length $2a$ are kept on a frictionless horizontal surface. When the mid point (P) of the string is pulled vertically upwards with a small but constant force $F$. the particles move towards each other on the surface. Magnitude of acceleration of each particle, when the separation between them becomes $2x$ is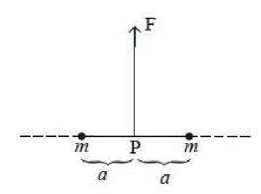
AP EAMCETAP EAMCET 2018
Solution:
