Q.
As shown in the figure, two blocks, each of mass $3\, kg$, are connected by a spring, whose spring constant is $200 \, N / m$. They are placed onto an inclined plane of angle $37^{\circ}$. The coefficient of friction between the upper block and the inclined plane is $0.6$, while between the lower block and the inclined plane is $0.1$. After a while, the two blocks move together with the same acceleration. Find the extension (in $cm$ ) of the spring. (Use $g=10\, m / s ^{2}$ )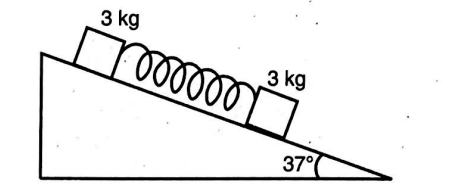
Laws of Motion
Solution: