Question

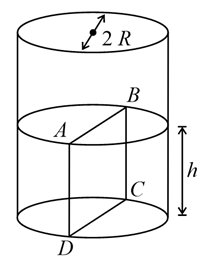
As shown in the figure below, there is a beaker of radius $R$ . Water is filled in the beaker up to a height $h$ . The density of water is $\rho $ , the surface tension of water is $T$ and the atmospheric pressure is $p_{0}$ . Consider a vertical section ABCD of the water column through a diameter of the beaker. What is the magnitude of the force on the water on one side of this section by the water on the other side of this section ?:

• A. $\left|\right. 2 p_{0} R h + \pi R^{2} \rho g h - 2 R T \left|\right.$
• B. $\left|\right. 2 p_{0} R h + R \rho g h^{2} - 2 R T \left|\right.$
• C. $\left|\right. p_{0} \pi R^{2} + R \rho g h^{2} - 2 R T \left|\right.$
• D. $\left|\right. p_{0} \pi R^{2} + R \rho g h^{2} + 2 R T \left|\right.$

Answer 1

Answer: (B)

Force from right hand side liquid on left hand side liquid,
(i) Due to surface tension force
= 2RT (towards right)
(ii) Due to liquid pressure force
$= \displaystyle \int _{\text{x} = 0}^{\text{x} = h} \left(\left(\text{p}\right)_{0} + \rho \text{gh}\right) \left(2 \text{R} \cdot \text{x}\right) \text{dx}$
= (2p₀Rh + Rρgh²) (towards left)
Net force is |2p₀Rh + Rρgh² - 2RT|