Question

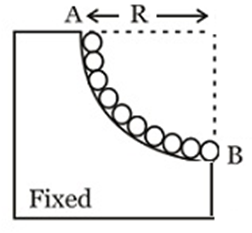
As shown in the figure, a chain of mass $m$ is placed on a smooth quarter circular portion of radius $R$ . End $A \, $ is tied with a wedge while the remaining chain is free, then the minimum work required to be done by the external agent to make the chain horizontal keeping point $A$ fixed, is

• A. $m\text{gR}$
• B. $m\text{g}\frac{2 \text{R}}{\pi }$
• C. $m\text{g}\sqrt{2}\frac{2 \text{R}}{\pi }$
• D. None

Answer 1

Answer: (B)

Center of mass of the chain is at $\frac{2 R}{\pi }$ from horizontal
As shown in figure .......
Height gain by center of mass is $\frac{2 \text{R}}{\pi }$



$\text{Wg}=-m\text{g}\left(\frac{2 \text{R}}{\pi }\right)$
$\mathrm{W}_{\text {ext. }}=-\mathrm{Wg}=\left(m \mathrm{~g} \frac{2 \mathrm{R}}{\pi}\right)$
Alternate solution



$\mathrm{U}_{\mathrm{i}}=\int-(\mathrm{dm}) \mathrm{gy}$
$=\text{g}\displaystyle \int \text{R cos}\theta \left(\frac{m}{\frac{\pi }{2}}\right)\text{d}\theta $
$=-\frac{2 \text{Rg} m}{\pi }\displaystyle \int _{0}^{\frac{\pi }{2}}cos\theta \text{d}\theta $
$=-\frac{2 \text{Rg} m}{\pi }\left[\right.\text{sin}\theta \left]\right._{0}^{\pi / 2}$
$=-\frac{2 m \text{gR}}{\pi }$
$\text{U}_{\text{f}}=0\Rightarrow \Delta \text{U}=\text{w}_{\text{ext}}=\frac{2 m \text{gR}}{\pi }$