Q.
As shown in the figure, a battery of emf $\epsilon$ is connected to an inductor $L$ and resistance R in series. The switch is closed at $t =0$. The total charge that flows from the battery, be tween $t = 0$ and $t = t_c$ ($t_c$ is the time constant of the circuit) is :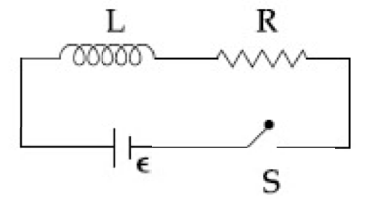
Solution: