Question

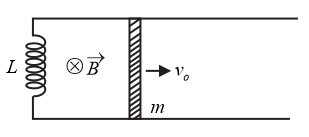
As shown in figure, the two parallel conducting rails, in a horizontal plane, are connected at one end by an inductor of inductance $ \, L$ . A slider (metallic) of mass $m$ , is imparted a velocity $v_{0}$ _, upon the rails, as shown in figure. The period of oscillation of the conducting rod is

• A. $\frac{\pi }{2}\frac{\sqrt{m L}}{B l}$
• B. $\frac{2 \pi \sqrt{m L}}{3 B l}$
• C. $\frac{2 \pi \sqrt{m L}}{B l}$
• D. $\frac{3 \pi \sqrt{m L}}{2 B l}$

Answer 1

Answer: (C)

From energy conservation (there are no dissipative forces)-
$E=\frac{1}{2}mv^{2}+\frac{1}{2}LI^{2}$
$\Rightarrow \frac{m}{2}\times 2v\frac{d v}{d t}+\frac{L}{2}\times 2I\frac{d I}{d t}=0$
$mv\frac{d v}{d t}=-IL\frac{d I}{d t}$
The emf induced in an inductor is
$E=L\frac{d I}{d t}=Blv$
$\Rightarrow L\frac{d I}{d t}=Bl\frac{d x}{d t}\Rightarrow LdI=Bldx\Rightarrow I=\frac{B l}{L}x$
The force acting on a current-carrying conductor is
$m\frac{d v}{d t}=-IBl$
$\Rightarrow \frac{d v}{d t}=-\frac{I B l}{m}$
Substituting the value of $I$ we get
$\frac{d v}{d t}=-\left(\frac{Bl}{L} x\right)\frac{B l}{m}\Rightarrow a=-\left(\frac{B^{2}l^{2}}{mL}\right)x$
We got acceleration in the form of
$a=-\omega ^{2}x$
this implies that the motion is SHM, with angular frequency
$\omega =\sqrt{\frac{B^{2} l^{2}}{m L}}$
The time period of motion is
$\Rightarrow \, \, T=2\pi \frac{\sqrt{m L}}{B l}$