Question

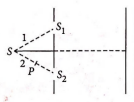
As shown in figure, a two slit arrangement with a source which emits unpolarised light. $P$ is a polariser with axis whose direction is not given. If $I_0$ is the intensity of the principal maxima when no polariser is present, calculate in the present case, the intensity of the principal maxima as well as of the first minima.

• A. $\frac{I_0}{8}$
• B. $\frac{3}{4}I_0$
• C. $\frac{I_0}{16}$
• D. $\frac{2}{5}I_0$

Answer 1

Answer: (A)

Without $P$:
$A= A_{\bot} +A_{||}$.
$A_{\bot}= A^{1}_{\bot} +A^{2}_{\bot} = A^{0}_{\bot} sin \left(kx -\omega t\right) + A^{0}_{\bot} sin\left(kx -\omega t +\phi\right)$
$A_{\left|\right|}$$= A_{\left|\right|}^{1}+A^{2}_{\left|\right|} = A_{\left|\right|}^{0} \left[ sin\left(kx-\omega t\right)+sin\left(kx-\omega t +\phi\right)\right] $
where $A^{0}_{\bot}, A^{0}_{||}$ are the amplitudes of either of the beam in $\bot$ and $||$ polarizations.
$\therefore $ Intensity $= \left\{\left|A^{0}_{\bot}\right|^{2} +\left|A_{\left|\right|}^{0}\right|^{2}\right\}[sin^{2}\left(kx -\omega t\right)$
$\left(1+cos^{2}\phi+2sin \phi\right)+sin^{2}\left(kx-\omega t\right)sin^{2}\phi]_{\text average}$
$ =\left\{\left|A^{0}_{\bot}\right|^{2} +\left|A_{\left|\right|}^{0}\right|^{2}\right\}\left(\frac{1}{2}\right)\cdot2\left(1+cos\phi\right)$
$ = 2 \left|A^{0}_{\bot}\right|^{2}\left(1+cos\phi\right), since \left|A_{\bot}^{0}\right|_{average} = \left|A^{0}_{\left|\right|}\right|_{average} $
With $P: $
Assume $A^{2}_{\bot}$ is blocked :
Intensity $= \left(A^{1}_{\left|\right|} + A^{2}_{\left|\right|}\right)^{2} + \left(A^{1}_{\bot}\right)^{2}$
$ = \left|A^{0}_{\bot}\right|^{2}\left(1+cos\phi\right) +\left|A^{0}_{\bot }\right|^{2} . \frac{1}{2} $
$ (I_{0} =4\left|A^{0}_{\bot }\right|^{2} $= Intensity without polariser at principal maxima )
Intensity at first maxima with polariser
$=\left|A_{\bot}^{0}\right|^{2} \left(2+\frac{1}{2}\right) $
$ = \frac{5}{8}I_{0}$
Intensity at first minima with polariser,
$ \left|A_{\bot }^{0}\right|^{2} \left(1-1\right) +\frac{\left|A_{\bot }^{0}\right|^{2}}{2}$
$ = \frac{I_{0}}{8}$