Q.
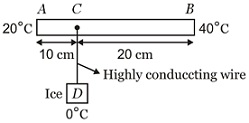
As shown in diagram, $AB$ is a rod of length $30 \, cm$ and area of cross section $1.0 \, cm^{2}$ and thermal conductivity $336 \, SI \, units$ . The ends $A$ and $B$ are maintained at temperatures $20 \,{}^\circ C$ and $40 \,{}^\circ C$ , respectively. A point $C$ of this rod is connected to a box $D$ , containing ice at $0 \,{}^\circ C$ , through a highly conducting wire of negligible heat capacity. The rate at which ice melts in the box is (assume latent heat of fusion for ice $L_{f}=80 \, cal \, g^{- 1}$ )
NTA AbhyasNTA Abhyas 2020Thermal Properties of Matter
Solution:
