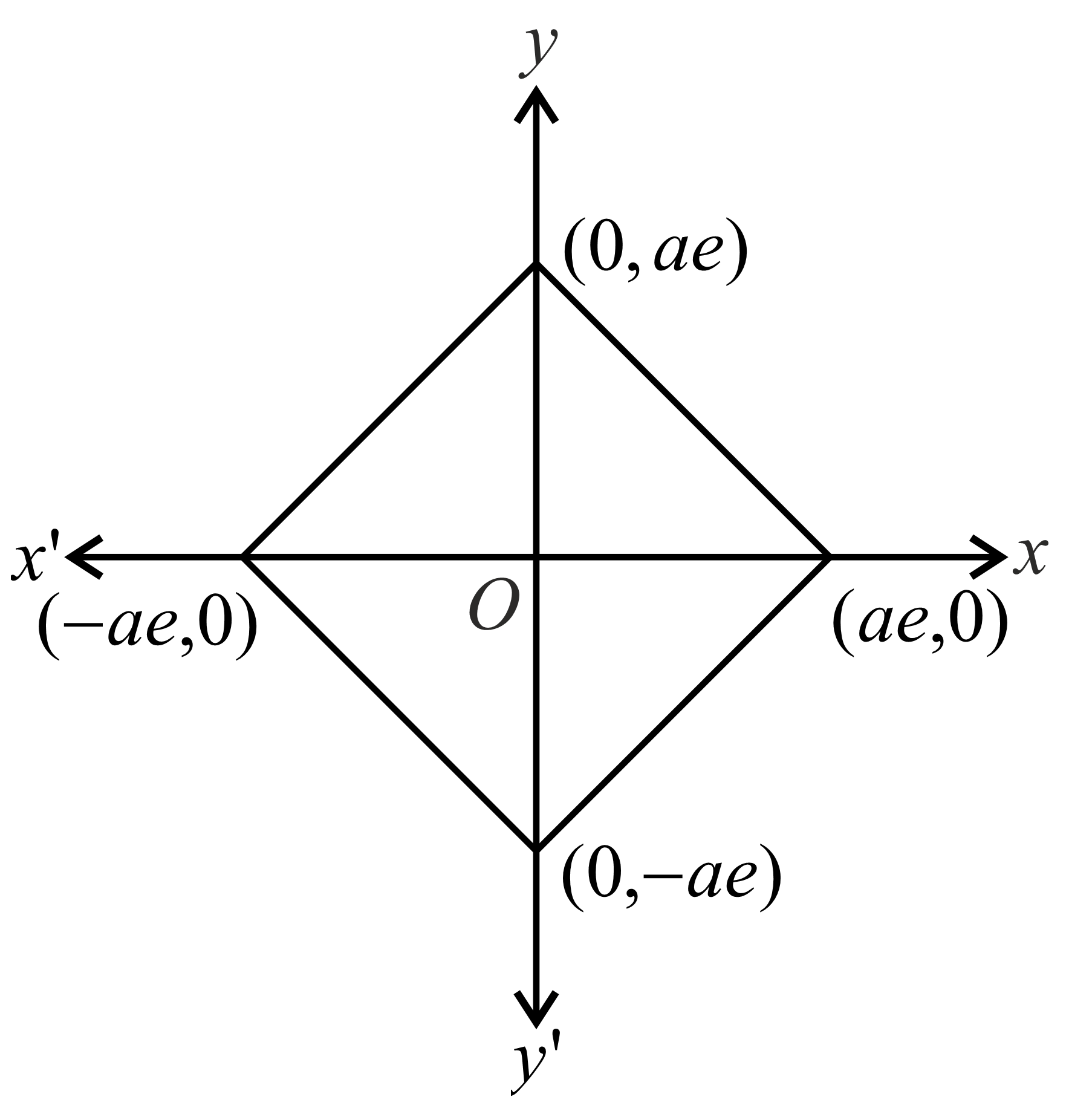
Question

Area of the quadrilateral formed with the foci of the hyperbolas $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ and $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=-1$ is $k\left(a^{2} + b^{2}\right)$ , then the value of $k$ is equal to

Answer 1

The foci are $\left(\pm a e , 0\right)\&\left(0 , \pm a e\right)$ .

The above diagram is a rhombus. Its area $=\frac{1}{2}d_{1}d_{2}$
$=\frac{1}{2}\left(2 a e\right)\left(2 a e\right)$
$=2a^{2}e^{2}$
We know that, $b^{2}=a^{2}\left(e^{2} - 1\right)$
$b^{2}=a^{2}e^{2}-a^{2}$
$b^{2}+a^{2}=a^{2}e^{2}$
So, area is $2\left(a^{2} + b^{2}\right)$ .