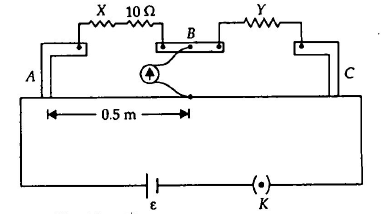
Q. An unknown resistance $X$ is connected in series with a resistance of $10 \, \Omega$. This combination connected in the left gap of the metre-bridge is balanced against another resistance $Y$ connected in the other gap. The balance point is found to be $0.50 \, m$. · When the $10 \, \Omega $ resistance is removed in the combination, the balance point is $0.4 \, m$. The value of $X$ in $\Omega$ is
Solution:
Given situation is shown in the figure.
$ \frac{X + 10}{Y} = \frac{50}{50}$
or, $X + 10 = Y$ ...(i)
Now, if $10 \, \Omega$ resistance is removed in the combination, the balance point is $0.4 \, m (= 40 \, cm)$ .
So, $ \frac{X}{Y} = \frac{40}{(100 - 40)} = \frac{2}{3}$
or, $Y = \frac{3}{2} X$ ...(ii)
From eqn (i) and (ii)
$X = 10 = \frac{3}{2} X $ or, $X = 20 \Omega $