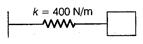
Q. An oscillator consists of a block attached to a spring $(k = 400 \,N/m)$. At some time t, the position (measured from the systems equilibrium location), velocity and acceleration of the block are $ x=0.100\,m,\,v=-15.0\,m/s $ , and $ a=-90\,m/s^{2} $ . The amplitude of the motion and the mass of the block are
AMUAMU 2013Oscillations
Solution:
Given that, spring constant $K=400 \,N / m$
Position $y=0.100\, m$
Velocity $V =-15.0\, m / s$
and acceleration $a =90 \,m / s ^{2}$
We know that $v=\omega \sqrt{A^{2}-y^{2}} \ldots$. (i)
and $a=-\omega^{2} y$ ... (ii)
From Eq. (ii), $90=\omega^{2} \times 0.1 $
$\Rightarrow \omega=30$
How $\omega^{2}=\frac{k}{m} 9\, \omega=\frac{400}{m} m=\frac{4}{9}=0.44 \,kg$
From Eq (i), $15=\omega \sqrt{A^{2}-y^{2}}$
$225=900\left(A^{2}-y^{2}\right)$
$ 225=900 A^{2}-900(0-1)^{2}$
$ A^{2}=\frac{234}{900} A=\frac{15}{30}$
$=\frac{1}{2}=0.5\, m$