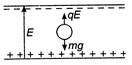
Q. An oil drop of radius $10^{-6} m$ carries charge equal to that of $3$ electrons. If density of the oil is $2 \times 10^{3} kg - m ^{3}$, then electric field required to keep the drop stationary is:
J & K CETJ & K CET 2002
Solution:
In order to keep the drop stationary.
For due to electric field = weight of the drop
$\therefore q E=m g$
$\Rightarrow E=\frac{m g}{q}=\frac{\text { volume } \times \text { density } \times g}{q}$
Given, $V=\frac{4}{3} \pi r^{3}=\frac{4}{3} \pi \times\left(10^{-6}\right)^{3}$
$\rho=2 \times 10^{3} kg m ^{-3},$
$g=10\, m / s ^{2},\, q=ne=3 \times 1.6 \times 10^{-19} C$
$\therefore E=\frac{4 \pi \times 10^{-18}}{3} \times \frac{2 \times 10^{3} \times 10}{3 \times 1.6 \times 10^{-19}}$
$\Rightarrow E=\frac{8 \times 3.14 \times 10^{5}}{9 \times 1.6}$
$\Rightarrow E=1.74 \times 10^{5} Vm ^{-1}$