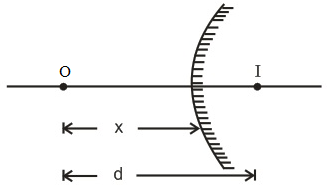
Question

An observer whose least distance of distinct vision is $d$ , views his own face in a convex mirror of radius of curvature $r$ . The magnification produced can not exceed?

• A. $\frac{\text{r}}{\text{d} + \sqrt{\text{r}^{2} + \text{d}^{2}}}$
• B. $\frac{\text{r}}{\text{d} + \sqrt{\text{d}^{2} - \text{r}^{2}}}$
• C. $\frac{\text{r}}{\text{d} - \sqrt{\text{r} + \text{d}}}$
• D. $\frac{\text{r}}{\text{d} + \sqrt{\text{d} + \text{r}}}$

Answer 1

Answer: (A)

Magnification, ​ $\text{m} = \frac{\text{f}}{\text{f} - \text{u}} \Rightarrow \text{m} = \frac{\text{f}}{\text{f} + \text{x}}$
$\text{m} = \frac{\text{r} / 2}{\text{r} / 2 + \text{x}} \Rightarrow \text{m} = \frac{\text{r}}{\text{r} + 2 \text{x}} \text{-------} \left(\text{1}\right)$
from mirror formula
$\frac{1}{\text{v}} + \frac{1}{\text{u}} = \frac{1}{\text{f}} \Rightarrow \frac{\text{1}}{\left(\right. \text{d} - \text{x} \left.\right)} + \frac{1}{- \text{x}} = \frac{1}{\text{f}} \Rightarrow \frac{1}{\text{d} - \text{x}} - \frac{1}{\text{x}} = \frac{2}{\text{r}}$
$\frac{+ \text{x} - \left(\right. \text{d} - \text{x} \left.\right)}{\text{x} \left(\right. \text{d} - \text{x} \left.\right)} = \frac{2}{\text{r}} \Rightarrow \left(2 \text{x} - \text{d}\right) \text{r} = 2 \text{x} \left(\text{d} - \text{x}\right)$
2rx - rd = 2xd - 2x² $⇒$ 2x² + 2(r - d)x - rd = 0
$\text{2} \left(\text{x}\right)^{2} + 2 \left(\text{r} - \text{d}\right) \text{x} - \text{r} \text{d} = 0 \Rightarrow \text{x} = \frac{- 2 \left(\text{r} - \text{d}\right) \pm \sqrt{\text{4} \left(\text{r} - \text{d}\right)^{2} + 8 \text{r} \text{d}}}{\text{4}}$
$\text{x} = \frac{2 \left(\text{d} - \text{r}\right) \pm \sqrt{\text{4} \left(\left(\text{r}\right)^{2} + \left(\text{d}\right)^{2}\right)}}{\text{4}} \Rightarrow \text{x} = \frac{\left(\text{d} - \text{r}\right) \pm \sqrt{\left(\left(\text{r}\right)^{2} + \left(\text{d}\right)^{2}\right)}}{\text{2}}$
$2 \text{x} = \left(\text{d} - \text{r}\right) \pm \sqrt{\left(\text{r}\right)^{2} + \left(\text{d}\right)^{2}}$
putting the value of x in equation (1)
$\text{m} = \frac{\text{r}}{\text{r} + \left[\right. \left(\text{d} - \text{r}\right) \pm \sqrt{\left(\text{r}\right)^{2} + \left(\text{d}\right)^{2}} \left]\right.}$
For m to be maximum, x should be minimum
$\text{m}_{\text{min}} = \frac{\text{r}}{\text{d} + \sqrt{\text{r}^{2} + \text{d}^{2}}}$