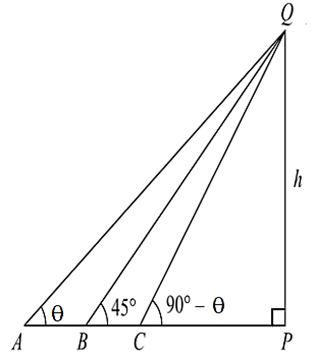
Question

An observer finds that the angular elevation of a tower is $\theta .$ On advancing $3m$ towards the tower, the elevation is $45^{o}$ and on advancing $2m$ further more towards the tower, the elevation is $90^{o}-\theta .$ The height of the tower is (assume the height of observer is negligible and observer lies on the same level as the foot of the tower)

• A. $2m$
• B. $4m$
• C. $6m$
• D. $8m$

Answer 1

Answer: (C)

Let, $PQ$ be the tower of height $h$ meters
$\angle PAQ=\theta ,\angle PBQ=45^{o}$ and $\angle PCQ=90^{o}-\theta $
$AB=3m$ and $BC=2m$

$\Rightarrow 3=AB=PA-PB=hcot A-h$
and $2=BC=PB-CP=h-htan A$
$\therefore \frac{h + 3}{h}=cot A,\frac{h - 2}{h}=tan ⁡ A$
$\therefore \frac{h + 3}{h}\cdot \frac{h - 2}{h}=1\Rightarrow h^{2}+h-6=h^{2}\Rightarrow h=6m$