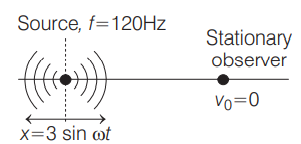
Question

An observer and a source emitting sound of frequency $120\, Hz$ are on the $X$ -axis. The observer is stationary while the source of sound is in motion given by the equation $x=3\, \sin \omega t(x$ is in metres and $t$ is in seconds). If the difference between the maximum and minimum frequencies of the sound observed by the observers is $22\, Hz$, then the value of $\omega$ is $\left(\right.$ speed of sound in air $=330\, ms ^{-1}$ )

• A. $33 \, rad \, s^{-1}$
• B. $36\, rad \, s^{-1}$
• C. $20\, rad \, s^{-1}$
• D. $10 \, rad \, s^{-1}$

Answer 1

Answer: (D)

Instantaneous speed of source is $v=\frac{d x}{d t}=3 \omega \sin \omega t$
Difference between maximum and minimum frequencies is $22 \,Hz$.
So, $f_{\max }-f_{\min }=f\left(\frac{v}{v-v_{s}}\right)-f\left(\frac{v}{v +v_{s}}\right)=22$
$\Rightarrow f\left\{\frac{v}{v-v_{s}}-\frac{v}{v+v_{s}}\right\}=22$ ...(i)
Now here, $f=120\, Hz ,\, v=330\, ms ^{-1},\, v_{s}=3 \omega$
Substituting these values in Eq (i), we get
$120\left(\frac{330}{330-3 \omega}-\frac{330}{330+3 \omega}\right)=22$
$\Rightarrow \omega=10\, s ^{-1}$