Q.
An object moves with a uniform velocity $u_{0}=5 \,m / s$ along the axis of a concave spherical mirror of focal length $f=-10\, cm$. If the object is at the centre of curvature $(C)$ at certain instant, then the magnitude of acceleration of image at this instant is $a m / s ^{2}$. Find $a$.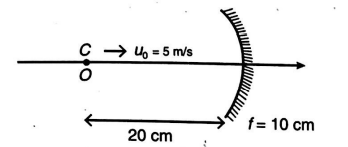
Ray Optics and Optical Instruments
Solution: