Question

An object is moving along a straight line as shown in the figure. It moves from $O$ to $P$ in $10\, s$ and returns from $P$ to $R$ in $20\, s$.

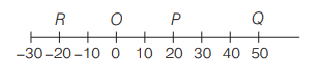
With reference to the above given figure, match the Column I (average velocity and average speed) with Column II (values) and select the correct answer from the codes given below.

Column I		Column II
A	The average velocity and the	1	$-0.5\, ms ^{-1}, 3 \, ms ^{-1}$ average speed of the object in going from $O$ to $P$ are
B	The average velocity and the	2	$+2 \, ms ^{-1}, 2\, ms ^{-1}$ average speed of the object in going from $O$ to $P$ and back to $R$ are
C	If the object moves from $O$ to $Q$ and back to $R$ in $40 \,s$, then	3	$-\frac{2}{3} ms ^{-1}, 2\, ms ^{-1}$ the average velocity and average speed of the object are

• A. $A - (1), B - (3), C - (2)$
• B. $A - (1), B - (2), C - (3)$
• C. $A - (2), B - (1), C - (3)$
• D. $A - (2), B - (3), C - (1)$

Answer 1

Answer: (D)

A. Here, average velocity $=\frac{\text { displacement }}{\text { time interval }}$
$=\frac{x_{2}-x_{1}}{t_{2}-t_{1}}=\frac{+20-0}{10\, s }=+2 \,ms ^{-1}$
Average speed $=\frac{\text { Total path length }}{\text { Time interval }} $
$=\frac{O P}{t_{2}-t_{1}}=\frac{20 m }{10 s }=2 \,ms ^{-1}$
B. For path travelled from $O$ to $P$ and and back to $R$, Average velocity $=\frac{\text { Displacement }}{\text { Time interval }}=\frac{x_{2}-x_{1}}{t_{2}-t_{1}}$
$=\frac{(-20)-0}{(10+20)}=-\frac{20}{30} ms ^{-1} $
$=-\frac{2}{3} ms ^{-1}$
Average speed $=\frac{\text { Path length }}{\text { Time interval }} $
$=\frac{O P+P R}{10+20} $
$=\frac{(20+40) m }{30 s }=\frac{60}{30} ms ^{-1}$
$=2 \,ms ^{-1}$
C. When object moves from $O$ to $Q$ and back to $R$, then Average velocity $=\frac{x_{2}-x_{1}}{t_{2}-t_{1}}=\frac{[(-20)-0] m }{40 \, s }$
$=-\frac{20}{40} ms ^{-1}=-0.5\, ms ^{-1}$
Average speed $=\frac{O Q+Q R}{\Delta t}$
$=\frac{(50+70) m }{40 s }=\frac{120}{40} ms ^{-1}=3\, ms ^{-1}$
Hence, $A \rightarrow 2, B \rightarrow 3$ and $C \rightarrow 1$.