Q.
An object is located $4\,m$ from the first of two thin converging lenses of focal lengths $2\,m$ and $1\,m$ respectively. The lenses are separated by $3\,m$. The final image formed by the second lens is located from the source at a distance of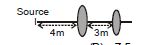
Solution: