1. Tardigrade
  2. Question
  3. Physics
  4. An L-shaped object, made of thin rods of uniform mass density, is suspended with a string as shown in figure. If AB = BC, and the angle made by AB with downward vertical is θ, then :

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

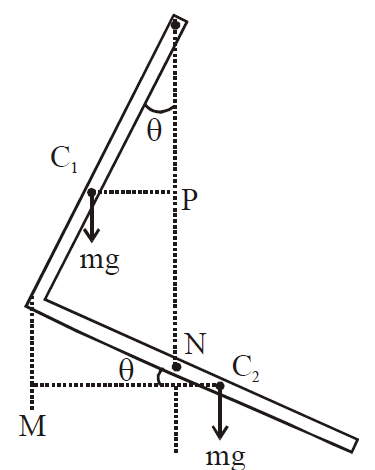
Q. An L-shaped object, made of thin rods of uniform mass density, is suspended with a string as shown in figure. If $AB = BC$, and the angle made by $AB$ with downward vertical is $\theta$, then :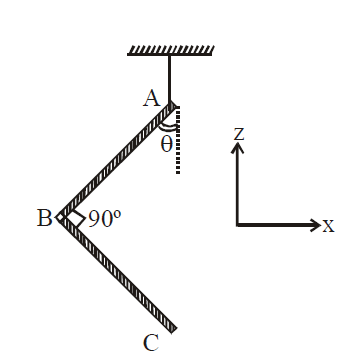Physics Question Image

JEE MainJEE Main 2019System of Particles and Rotational Motion

Solution:

Let mass of one rod is $m$.
Balancing torque about hinge point.
$mg \left(C_{1}P\right) = mg \left(C_{2}N\right) $
$ mg \left(\frac{L}{2} \sin\theta\right) = mg \left(\frac{L}{2} \cos\theta - L \sin\theta\right) $
$ \Rightarrow \frac{3}{2} mg L \sin\theta = \frac{mgL}{2} \cos\theta $
$ \Rightarrow \tan \theta = \frac{1}{3} $

Solution Image