Q.
An isosceles triangle is formed with a thin rod of length $l_{1}$ and coefficient of linear expansion $\alpha_{1}$, as the base and two thin rods each of length $l_{2}$ and coefficient of linear expansion $\alpha_{2}$ as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. The ratio of lengths $\frac{l_{1}}{l_{2}}$ is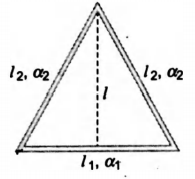
Thermal Properties of Matter
Solution:
