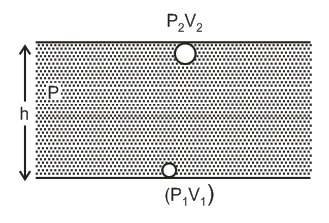
Question

An inverted bell, lying at the bottom of lake $47.6 \, m$ deep, has $50 \, cm^{3}$ of air trapped in it. The bell is brought to the surface of the lake, then the volume of the trapped air will become [atmospheric pressure = $70 \, cm$ of $Hg$ and density of $Hg=13.6 \, g \, cm^{- 3}$ ]

• A. $600cm^{3}$
• B. $300 \, cm^{3}$
• C. $250cm^{3}$
• D. $200cm^{3}$

Answer 1

Answer: (B)

According to Boyle's law, pressure and volume are inversely proportional to each other i.e. $\text{p} \propto \frac{1}{\text{v}}$

$\Rightarrow P_{1}V_{1}=P_{2}V_{2}$
$\Rightarrow \left(\right.P_{0}+h\left(\rho \right)_{\text{w}}g\left.\right)V_{1}=P_{0}V_{2}$
$\Rightarrow V_{2}=\left(\right.1+\frac{\left(hρ\right)_{\text{w}} g}{P_{0}}\left.\right)V_{1}$
$V_{2}=\left(\right.1+\frac{47.6 \star 1 \star 1000 \star 10}{70 \star \left(10\right)^{- 2} \star 13.6 \star 1000 \star 10}\left.\right) \\ \\ \left[\right.As \, P_{2}=P_{0}=70 \, cm \, of \, Hg=70\star\left(10\right)^{- 2}\star13.6\star1000\star10\left]\right. \\ $
$\Rightarrow \left(\text{V}\right)_{2}=\left(1 + 5\right)50\left(\text{cm}\right)^{3}=300\left(\text{cm}\right)^{3}$