Q.
An insulated container has a partition wall to divide it into two compartments $I$ and $II$ . The partition wall can move without any friction and it is conducting. Same gas fills the two compartments. Initial parameters for both compartments are shown in the figure. Find the incorrect option at the equilibrium position.
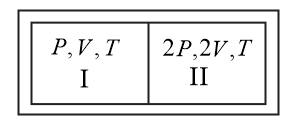
NTA AbhyasNTA Abhyas 2020
Solution:
For any closed system, number of moles remain conserved.
$n_{1}+n_{2}=n_{1}^{'}+n_{2}^{'}$
Here $n_{1},n_{2 =}$ initial moles
and $n_{1}^{'},n_{2}^{'}=$ final moles
when piston comes in equilibrium, Final pressure and final temperature becomes equal.
From the ideal gas equation we know that
$PV=nRT$
where $n=$ number of moles
Putting the values of number of moles in above equation gives
$\frac{P V}{R T}+\frac{2 P \cdot 2 V}{R T}=\frac{P^{'}}{R T}\left[\right.3V\left]\right.\Rightarrow P^{'}=\frac{5 P}{3}$
Here $P^{'}$ =final pressure
For left chamber,
$PV=P^{'}V^{'}=\frac{5 P}{3}V^{'}\Rightarrow V^{'}=\frac{3 V}{5}$
For right chamber,
$4PV=P^{'}V^{'}=\frac{5 P}{3}V^{'}\Rightarrow V^{'}=\frac{12 V}{5}$
$n_{1}+n_{2}=n_{1}^{'}+n_{2}^{'}$
Here $n_{1},n_{2 =}$ initial moles
and $n_{1}^{'},n_{2}^{'}=$ final moles
when piston comes in equilibrium, Final pressure and final temperature becomes equal.
From the ideal gas equation we know that
$PV=nRT$
where $n=$ number of moles
$\frac{P V}{R T}+\frac{2 P \cdot 2 V}{R T}=\frac{P^{'}}{R T}\left[\right.3V\left]\right.\Rightarrow P^{'}=\frac{5 P}{3}$
Here $P^{'}$ =final pressure
For left chamber,
$PV=P^{'}V^{'}=\frac{5 P}{3}V^{'}\Rightarrow V^{'}=\frac{3 V}{5}$
For right chamber,
$4PV=P^{'}V^{'}=\frac{5 P}{3}V^{'}\Rightarrow V^{'}=\frac{12 V}{5}$