1. Tardigrade
  2. Question
  3. Physics
  4. An insect crawls up a hemispherical surface very slowly. The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle a with the vertical, the maximum possible value of a so that the insect does not slip is given by

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

Q. An insect crawls up a hemispherical surface very slowly. The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle a with the vertical, the maximum possible value of a so that the insect does not slip is given by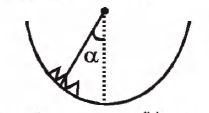Physics Question Image

AIEEEAIEEE 2012Laws of Motion

Solution:

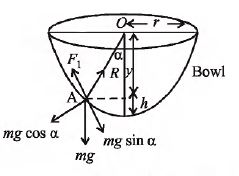
The insect crawls up the bowl upto a certain height h only till the component of its weight along the bowl is balanced by limiting frictional force.
For limiting condition at point A
$R = mg \,cos \,\alpha \quad\quad...\left(i\right)$
$F_{1} = mg\, sin \,\alpha\quad\quad ...\left(ii\right)$
Dividing eq. $\left(ii\right)$ by $\left(i\right)$
$tan\,\alpha = \frac{1}{cot\,\alpha} = \frac{F_{1}}{R} = \mu\left[As\,F_{1} =\mu R \right]$
$\Rightarrow \quad tan\,\alpha =\mu = \frac{1}{3} [\because\,\mu($Given$] ) $
$\therefore \quad cot \,\alpha = 3$

Solution Image