Q.
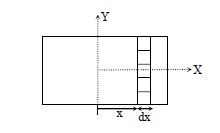
An infinitely long uniform line charge distribution of charge per unit length $λ$ lies parallel to the y-axis in the y-z plane at z = $\frac{\sqrt{3}}{2}$ a (see figure). If the magnitude of the flux of the electric field through the rectangular surface ABCD lying in the x-y plane with its centre at the origin is $\frac{\lambda L}{nε_{0}}$ ($ε_{0}$ = permittivity of free space), then the value of n is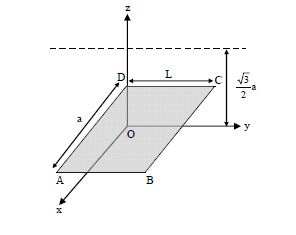
Solution:
Electric flux though elemental part -
$d\phi = EdA \,cosθ$
$d\phi = \frac{\lambda}{2\pi\in_{0}\sqrt{x^{2}+\frac{3a^{2}}{4}}}\times Ldx \times \frac{\frac{\sqrt{3a}}{2}}{\sqrt{x^{2}+\frac{3a^{2}}{4}}}$
$\int d\phi = \frac{\sqrt{3}a\lambda L}{4\pi\in_{0}} \int\limits^{a / 2}_{x = -\frac{a}{2} \frac{dx}{\left(x^{2}+\frac{3a^{2}}{4}\right)}}$
$\phi = \frac{\sqrt{3}a\lambda L}{4\pi\in_{0}}\times2\quad\int\limits^{a / 2}_{0} \frac{dx}{x^{2}+\frac{3a^{2}}{4}}$
$\phi = \frac{\sqrt{3}a\lambda L}{2\pi \in _{0}}\times \frac{2}{\sqrt{3a}}\left[tan^{-1}\left(\frac{2x}{\sqrt{3}a}\right)\right]^{a / 2}_{0}$
$\phi = \frac{\lambda L}{\pi\in_{0}} tan^{-1}\left(\frac{1}{\sqrt{3}}\right)$
$\phi = \frac{\lambda L}{6 \in_{0}}$
On comparing $n = 6$