Q.
An infinitely long solid cylinder of radius $R$ has a uniform volume charge density $\rho$. It has a spherical cavity of radius $R / 2$ with its centre on the axis of the cylinder, as shown in the figure. The magnitude of the electric field at the point $P$, which is at a distance $2 R$ from the axis of the cylinder, is given by the expression $\frac{23 \rho R}{16 n \varepsilon_{0}} .$ The value of $n$ is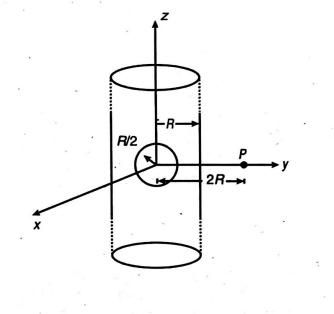
Electric Charges and Fields
Solution: