Question

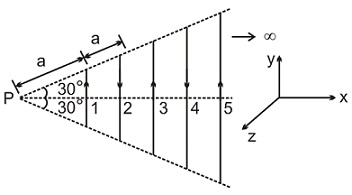
An infinite number of straight wires each carrying current $I$ are equally placed as shown in the figure. Adjacent wires have current in the opposite direction. The net magnetic field at point $P$ is

• A. $\frac{\mu _{0} I}{4 \pi }\frac{l \text{n} 2}{\sqrt{3} a}\hat{\text{k}}$
• B. $\frac{\mu _{0} I}{4 \pi }\frac{\text{ln} 4}{\sqrt{3} a}\hat{\text{k}}$
• C. $\frac{\mu_0 I \ln 4}{4 \pi \sqrt{3} a}(-\hat{\mathrm{k}})$
• D. Zero

Answer 1

Answer: (B)

$\mathrm{B}_1=\frac{\mu_0 I}{4 \pi^a}(\sin \alpha+\sin \beta)=\frac{\mu_0}{4 \pi} \frac{I \times 2 \sin 30^{\circ}}{a \cos 30^{\circ}}$
$\overset{ \rightarrow }{\text{B}} = \overset{ \rightarrow }{\text{B}} = \text{B}_{1} \hat{\text{k}} + \text{B}_{2} \hat{\text{k}} + \text{B}_{3} \hat{\text{k}} - \text{B}_{4} \hat{\text{k}} + \text{.....}$
$=\frac{\mu _{0}}{4 \pi }\frac{I \times 2 sin 3 0^{^\circ }}{a cos 3 0^{^\circ }}\hat{\text{k}}-\frac{\mu _{0}}{4 \pi }\frac{I \times 2 sin 3 0^{^\circ }}{2 a cos 3 0^{^\circ }}\hat{\text{k}}+\frac{\mu _{0}}{4 \pi }\frac{I \times 2 sin 3 0^{^\circ }}{3 a cos 3 0^{^\circ }}\hat{\text{k}}+\text{.....}$
$=\frac{\mu _{0}}{4 \pi }\frac{2 I}{\sqrt{3} a}\hat{\text{k}}-\frac{\mu _{0}}{4 \pi }\frac{2 I}{\sqrt{3} \times 2 a}\hat{\text{k}}+\frac{\mu _{0}}{4 \pi }\frac{2 I}{\sqrt{3} \times 3 a}\hat{\text{k}}+\text{.....}$
$=\frac{\mu_0 \quad 2 I}{4 \pi \sqrt{3} a}\left[1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\ldots\right] \hat{\mathrm{k}}=\frac{\mu_0 2 I}{4 \pi \sqrt{3} a} \log _{\mathrm{e}}(1+1) \hat{\mathrm{k}}=\frac{\mu_0 2 I}{4 \pi \sqrt{3} a} \log _{\mathrm{e}} 2 \hat{\mathrm{k}}$
$=\left(\frac{\mu_0 I}{4 \pi \sqrt{3} a} \log _{\mathrm{e}} 4\right) \hat{\mathrm{k}}$