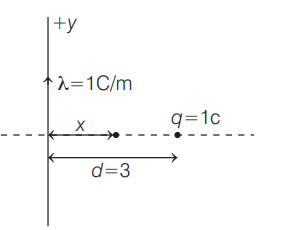Question

An infinite line of charge with uniform line charge density of $1\, C / m$ is palced along the $y$ -axis. A charge of $1\, C$ is placed on the $x$ -axis at a distance of $d=3\, m$ from the origin. At what distance $r$ from the origin on the $x$ -axis, the total electric field is zero. (Assume, $0 < r < d$ )

• A. 1 m
• B. 2 m
• C. 2.5 m
• D. 1.75 m

Answer 1

Answer: (B)

An infinite line of uniform charge density is placed along $y$ -axis and a charge $(+1\, C)$ is placed at $x=+3\, m$, as shown in the figure. For electric field to be zero at $x$, there should be
$E _{\text {line charge }}= E _{\text {point charge }}$ ...(i)
As we know, for line charge
$E _{\text {line charge }}=\frac{2 k \lambda}{x}=\frac{2 k}{x}$ ...(ii)
Similarly, for point charge,
$E _{\text {point charge }}=\frac{k q}{(3-x)^{2}}=\frac{k}{(3-x)^{2}}$ ...(iii)
From Eqs. (i), (ii) and (iii), we get
$\frac{2 k}{x}=\frac{k}{(3-x)^{2}}$
$\Rightarrow \frac{2}{x}=\frac{1}{(3-x)^{2}}$
$\Rightarrow 2 x^{2}-13 x+ 18=0$
This is a quadratic equation, which have solution
$x_{1}, x_{2}=\frac{13 \pm \sqrt{13^{2}-144}}{4}$
So, $x_{1}=4.5\, m$ (not possible, as $0< x<3$ ) and $x_{2}=2\, m$