1. Tardigrade
  2. Question
  3. Physics
  4. An inductor of inductance L = 400 mH and resistors of resistances R1 = 2Ω and R2 = 2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t = 0. The potential drop across L as a function of time is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

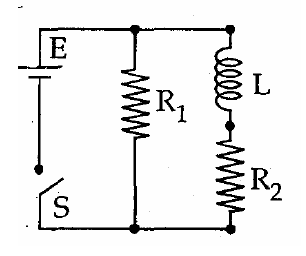
Q. An inductor of inductance $L = 400\, mH$ and resistors of resistances $R_1 = 2Ω$ and $R_2 = 2\Omega$ are connected to a battery of emf $12\,V$ as shown in the figure. The internal resistance of the battery is negligible. The switch $S$ is closed at $t = 0$. The potential drop across $L$ as a function of time is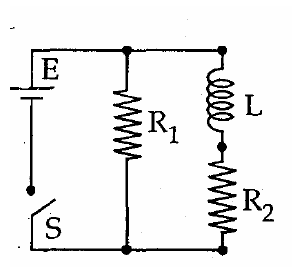Physics Question Image

AIEEEAIEEE 2009Alternating Current

Solution:

$I_{1}=\frac{F}{R_{1}}=\frac{12}{2}=6A$
$E=L \frac{dI_{2}}{dt}+R_{2}\times I_{2}$
$I_{2}=I_{o}\left(1-e^{-t/t_{c}}\right) \Rightarrow I_{o}=\frac{E}{R_{2}}=\frac{12}{2}=6A$
$t_{c}=\frac{L}{R}=\frac{400\times10^{-3}}{2}=0.2$
$I_{2}=6\left(1-e^{t/0.2}\right)$
Potential drop across $L = E - R_{2}I_{2} = 12 - 2 × 6\left(1-e^{-bt}\right)=12\,e^{-5t}$
Directions: Question numbers 28, 29 and 30 are based on the following paragraph. Two moles of helium gas are taken over the cycle ABCDA, as shown in the P - T diagram.

Solution Image Solution Image