Q.
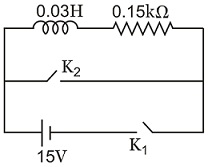
An inductor $\left(\right. L = 0.03 \, \text{H} \left.\right)$ and a resistor $( R = 0.15 \, {k \Omega } )$ are connected in series to a battery of $15 \, \text{V}$ EMF in a circuit shown below. The key $K_{1}$ has been kept closed for a long time. Then at $t=0$ , $K_{1}$ is opened and key $K_{2}$ is closed simultaneously. At $t=1 \, \text{ms}$ , the current in the circuit will be : $e^{5}\cong150$
NTA AbhyasNTA Abhyas 2020
Solution:

