Q.
An inclined plane makes an angle of $30^{\circ}$ with the horizontal electric field $E$ of $100\, V / m$. A particle of mass $1 kg$ and charge $0.01 \,C$ slides down from a height of $1\, m$. If the coefficient of friction is $0.2$, find the time taken for the particle to reach the bottom. (in sec)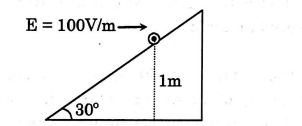
Electrostatic Potential and Capacitance
Solution:
