Question

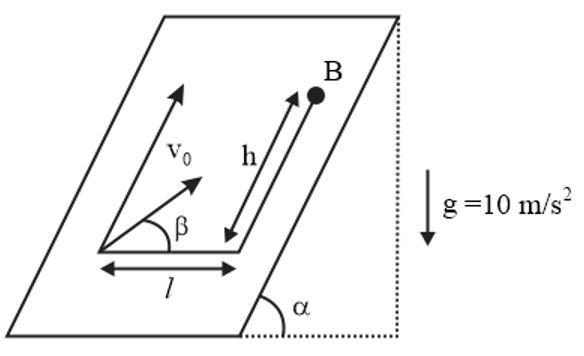
An inclined plane is located at angle $\alpha =53^{\circ} $ to the horizontal. There is a hole at point $B$ in the inclined plane as shown in the figure. A particle is projected along the plane with speed $v_{0}$ at an angle $\beta =37^{\circ} $ to the horizontal in such a way so that it gets into the hole. Neglect any type of friction. Find the speed $v_{0}$ (in $ms^{- 1}$ ) if $h=1m$ and $l=8m$ .

• A. 9
• B. 3
• C. 6
• D. 12

Answer 1

Answer: (A)

$ h =l \tan \beta-\frac{1}{2} \frac{g \sin \alpha l^{2}}{v_{0}^{2} \cos ^{2} \beta} $
$ v_{0} =\sqrt{\frac{g \sin \alpha l^{2}}{2 \cos ^{2} \beta(l \tan \beta-h)}} $
$ =\sqrt{\frac{10 \times \frac{4}{5} \times 8 \times 8}{2 \times \frac{4}{5} \times \frac{4}{5}\left(8 \times \frac{3}{4}-1\right)}}=9 \,m \, s ^{-1}$