Question

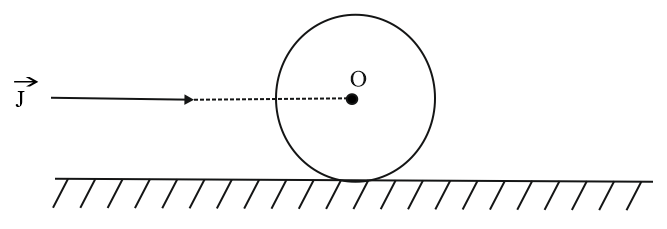
An impulse $\text{J}$ is applied on a ring of mass $\text{m}$ along a line passing through its centre $\text{O}$ . The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is

• A. $\frac{\text{J}}{\text{m}}$
• B. $\frac{\text{J}}{\text{2m}}$
• C. $\frac{\text{J}}{\text{4m}}$
• D. $\frac{\text{J}}{\text{3m}}$

Answer 1

Answer: (B)

Let $\text{v}$ be the velocity of COM of the ring just after the impulse is applied and $\text{v'}$ is the velocity when pure rolling starts.
Angular velocity $\text{ω}$ of the ring at this instant will be $\omega = \frac{\text{v'}}{\text{r}}$
$\Rightarrow $ Impulse = change in linear momentum
we have, $\text{J} = \text{mv}$
or $\text{v=J/m}$
Between the two positions shown in figure force of
friction on the ring acts backwards. Angular momentum
of the ring about bottommost point will remain conserved
$\therefore \, \text{L}_{\text{i}} = \text{L}_{\text{f}}$
or $\text{mvr} = \text{mv'r} + \text{l} \omega $
$= \text{mv' r +} \left(\left(\text{mr}\right)^{2}\right) \frac{\text{v'}}{\text{r}} = 2 \text{mv' r}$
$\therefore $ $\text{v'} = \frac{v}{2} = \text{J/2m}$