Q.
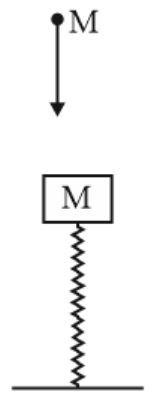
An ideal spring supports a disc of mass $M$ . A body of mass $m$ is released from a certain height from where it falls to hit $M$ . The two masses stick together at the moment they touch and move together from then on. The oscillations reach to a height $a$ above the original level of the disc and depth $b$ below it. The constant of the force of the spring is
NTA AbhyasNTA Abhyas 2020Oscillations
Solution: