Q.
An ideal monoatomic gas is confined in a cylinder by a spring loaded piston of cros section $8.0 \times 10^{-3} \, m^2$. Initially the gas is at 300K and occupies a volume of $2.4 \times 10^{-3} \, m^3$ and the spring is in its relaxed state as shown in figure. The gas is heated by a small heater until the piston moves out slowly by $0.1\, m$. The force constant of the spring is $8000\, N/m$ and the atmospheric pressure is $1.0 \times 10^5 \, N/m^2$. The cylinder and the piston are thermally insulated. The piston and the spring are massless and there is no friction between the piston and the cylinder. The final temperature of the gas will be :
(Neglect the heat loss through the lead wires of the heater. The heat capacity of the heater coil is also negligible)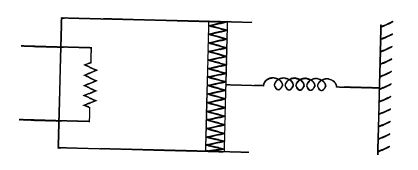
Solution: