Q.
An ideal gas is undergoing a cyclic thermodynamic process in different ways as shown in the corresponding $𝑃 − 𝑉$ diagrams in column 3 of the table. Consider only the path from state 1 to state 2. 𝑊 denotes the corresponding work done on the system. The equations and plots in the table have standard notations as used in thermodynamic processes. Here $γ$ is the ratio of heat capacities at constant pressure and constant volume. The number of moles in the gas is $𝑛$.
Column 1
Column 2
Column 3
(I) $W _{1 \rightarrow 2}=\frac{1}{\gamma-1}\left( P _{2} V _{2}- P _{ I } V _{1}\right)$
(i) Isothermal
(P) 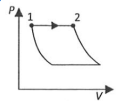
(II) $W _{1 \rightarrow 2}=- PV _{2}+ PV _{1}$
(ii) Isochoric
(Q) 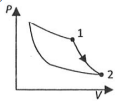
(III) $W_{1\to 2} = 0$
(iii) Isobaric
(R)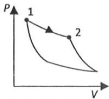
(IV)$W _{ l \rightarrow 2}=- nRT ^{\prime} n \left(\frac{ V _{2}}{ V _{1}}\right)$
(iv) Adiabatic
(S) 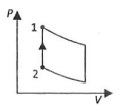
Which one of the following options correctly represents a thermodynamic process that is used as a correction in the determination of the speed of sound in an ideal gas?
| Column 1 | Column 2 | Column 3 |
|---|---|---|
| (I) $W _{1 \rightarrow 2}=\frac{1}{\gamma-1}\left( P _{2} V _{2}- P _{ I } V _{1}\right)$ | (i) Isothermal | (P)  |
| (II) $W _{1 \rightarrow 2}=- PV _{2}+ PV _{1}$ | (ii) Isochoric | (Q)  |
| (III) $W_{1\to 2} = 0$ | (iii) Isobaric | (R) |
| (IV)$W _{ l \rightarrow 2}=- nRT ^{\prime} n \left(\frac{ V _{2}}{ V _{1}}\right)$ | (iv) Adiabatic | (S)  |
JEE AdvancedJEE Advanced 2017
Solution: