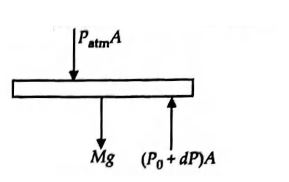
Question

An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass $M$ . The piston and the cylinder have equal cross sectional area $A$. When the piston is in equilibrium, the volume of the gas is $V_{0}$ and its pressure is $P_{0}$ The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency

• A. $\frac{1}{2\pi} \sqrt{\frac{MV_{0}}{A\gamma P_{0}}}$
• B. $\frac{1}{2\pi} \frac{A\gamma P_{0}}{V_{0}M}$
• C. $\frac{1}{2\pi} \frac{V_{0}MP_{0}}{A^{2}\gamma}$
• D. $\frac{1}{2\pi} \sqrt{\frac{A^{2}\gamma P_{0}}{MV_{0}}}$

Answer 1

Answer: (D)

$FBD$ of piston at equilibrium

$P _{atm}A+Mg=P_{0}A$ $\ldots\left(i\right)$
$FBD$ of piston when piston is pushed down a distance $x$

$\left(P_{0}+dp\right)A-\left(p_{atm} A+Mg\right)=M \frac{d^{2}x}{dt^{2}} \ldots\left(ii\right)$
As the system is completely isolated from its surrounding therefore the change is adiabatic
For an adiabatic process
$PV^{\gamma}$ =constant $ \therefore V^{\gamma} dP+P\gamma V^{\gamma-1} dV=0$
or $dP=-\frac{\gamma PdV}{V} $
$\therefore dp=-\frac{\gamma P_{0} \left(Ax\right)}{V_{0}} \ldots\left(iii\right)$
Using $\left(i\right)$ and $\left(iii\right)$ in $\left(ii\right)$, we get
$M \frac{d^{2} x}{dt^{2}}=-\frac{\gamma P_{0}A^{2}}{V_{0}}x $
or $ \frac{d^{2}x}{dt^{2}}=-\frac{\gamma P_{0}A^{2}}{MV_{0}}x$
Comparing it with standard equation of $SHM$,
$\frac{d^{2}x}{dt^{2}}=-\omega^{2}x$
We get,$ \omega^{2}=\frac{\gamma P_{0}A^{2}}{MV_{0}}$ or $\omega=\sqrt{\frac{\gamma P_{0} A^{2}}{MV_{0}}}$
Frequency, $\upsilon=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{\gamma P _{0}A^{2}}{MV_{0}}}$