Question

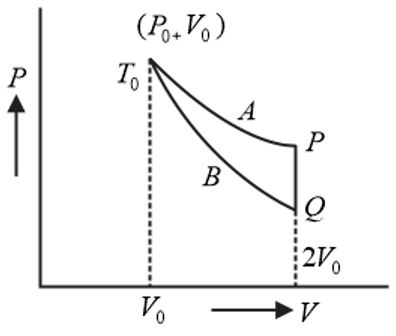
An ideal gas ( $1$ mole, monatomic) is in the initial state $P$ (see diagram) on an isothermal curve $A$ at a temperature $T_{0}$ . It is brought under a constant volume $\left(2 V_{0}\right)$ process to $Q$ which lies on an adiabatic curve $B$ intersecting the isothermal curve $A$ at $\left(P_{0} , \, V_{0} , \, T_{0}\right)$ . The change in the internal energy of the gas (in terms of $T_{0}$ ) during the process is $\left(2^{2/3} = \text{1.587}\right)$

• A. $\text{2.3}T_{0}$
• B. $\text{-4.6}T_{0}$
• C. $\text{-2.3}T_{0}$
• D. $\text{4.6}T_{0}$

Answer 1

Answer: (B)

Temperature at state $P=T_{0}$ , since $P$ lies on the isotherm of temperature $T_{0}$ . If $T$ be the temperature at $Q$ , then for the adiabatic process $B$ , we have $T_{0}V_{0}^{\gamma - 1}=T\left(2 V_{0}\right)^{\gamma - 1}$
$T=\frac{T}{2^{\gamma - 1}}=\frac{T_{0}}{2^{2 / 3}}$
Change in the internal energy of the gas is
$\Delta U=C_{V}\left(T - T_{0}\right)=\left(\frac{R}{- 1}\right)\left(\frac{T_{0}}{2^{2 / 3}} - T_{0}\right)$
$=\frac{3 R T_{0} \left(1 - 2^{2 / 3}\right)}{2 \times 2^{2 / 3}}=-\text{4.6}T_{0}$