Q.
An ideal fluid of density $800\, kgm ^{-3}$, flows smoothly through a bent pipe (as shown in figure) that tapers in cross-sectional area from a to $\frac{ a }{2}$. The pressure difference between the wide and narrow sections of pipe is $4100\, Pa$. At wider section, the velocity of fluid is $\frac{\sqrt{x}}{6} ms ^{-1}$ for $x =$ (Given $g=10\, m ^{-2}$ )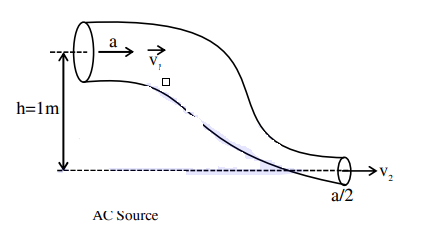
Solution: