Q.
An ideal fluid flows in the pipe as shown in the figure. The pressure in the fluid at the bottom $P_{2}$ is the same as it is at the top $P_{1}$. If the velocity of the top $v_{1}=2\, m / s$. Then the ratio of areas $A_{1} \cdot A_{2}$ is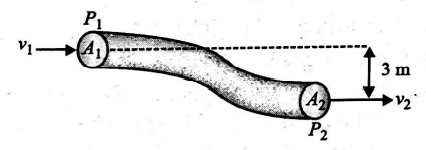
Mechanical Properties of Fluids
Solution: