Question

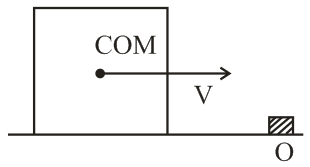
An ice cube of mass $M$ and with sides of length a is sliding without friction with speed $v_{0}$ when it hits a ridge $O$ at the edge of counter (see figure). This collision causes the cube to tilt as shown. The minimum value of $v_{0}$ needed for the cube to fall off the table is given by $\sqrt{kag}.$ Find value of $k.$ (Approximate the answer to nearest integer.)

Answer 1

$Mv _{0}\left(\frac{ a }{2}\right)= I _{0} \omega$ (apply COAM)
$=\left(\frac{ Ma ^{2}}{6}+ M \left(\frac{ a }{\sqrt{2}}\right)^{2}\right) \omega \Rightarrow \omega=\frac{3 v _{0}}{4 a }$
Now, from conservation of energy.
$\frac{1}{2}I\left(\omega \right)^{2}=mg\left(\right.\Delta h\left.\right)$
$\Rightarrow \frac{1}{2}\left(\frac{2}{3} \left(Ma\right)^{2}\right]\left(\left(\frac{3 v_{0}}{4 a}\right]\right)^{2}=Mg\left(\frac{a}{\sqrt{2}} - \frac{a}{2}\right)$
$\Rightarrow v_{0}=\sqrt{1 . 1 ag}$