Question

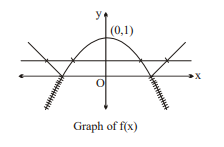
An even polynomial function $f (x)$ satisfies a relation
$f(2 x)\left(1-f\left(\frac{1}{2 x}\right)\right)+f\left(16 x^2 y\right)=f(-2)-f(4 x y) \forall x, y \in R-\{0\}$ and $f(4)=-255, f(0)=1$Which of the following hold(s) good?

• A. $f(x)$ has local maximum at $x=1$.
• B. $f(x) f\left(\frac{1}{x}\right) \leq 0$
• C. Range of values of $k$ for which $|f(x)|=k-2$ has exactly four distinct solutions is $(2,3)$.
• D. $\int_0^1 f ( x ) dx =\frac{3}{4}$.

Answer 1

Answer: (B), (C)

We have $f(2 x)-f(2 x) f\left(\frac{1}{2 x}\right)+f\left(16 x^2 y\right)=f(-2)-f(4 x y)$
Replacing y by $\frac{1}{8 x^2}$, we get
$f(2 x)-f(2 x) f\left(\frac{1}{2 x}\right)+f(2)=f(-2)-f\left(\frac{1}{2 x}\right)$
$f(2 x)+f\left(\frac{1}{2 x}\right)=f(2 x) f\left(\frac{1}{2 x}\right) ($ As $f(x)$ is even)
$\therefore f (2 x )=1 \pm(2 x )^{ n }$
$\Rightarrow f ( x )=1 \pm x ^{ n }$
Now $f(4)=1 \pm 4^{ n }=-255 $ (Given)
Taking negative sign, we get $256=4^{ n } \Rightarrow n =4$
Hence $f(x)=1-x^4$, which is even function.
Now $| f ( x )|= k -2$
$\Rightarrow 0< k -2<1 \Rightarrow 2< k <3$
Clearly $f ( x )$ has local maximum at $x =0$.

Also $\int\limits_0^1 f(x) d x=\int\limits_0^1\left(1-x^4\right) d x=\left(1-\frac{x^5}{5}\right)_0^1=1-\frac{1}{5}=\frac{4}{5}$.