Q.
An equilateral triangular loop $ADC$ having some resistance is pulled with a constant velocity $v$ out of a uniform magnetic field directed into the screen. At the time $t=0$ , side $DC$ of the loop is at the edge of the magnetic field. The induced current $\left(i\right)$ versus time $\left(t\right)$ graph will be as
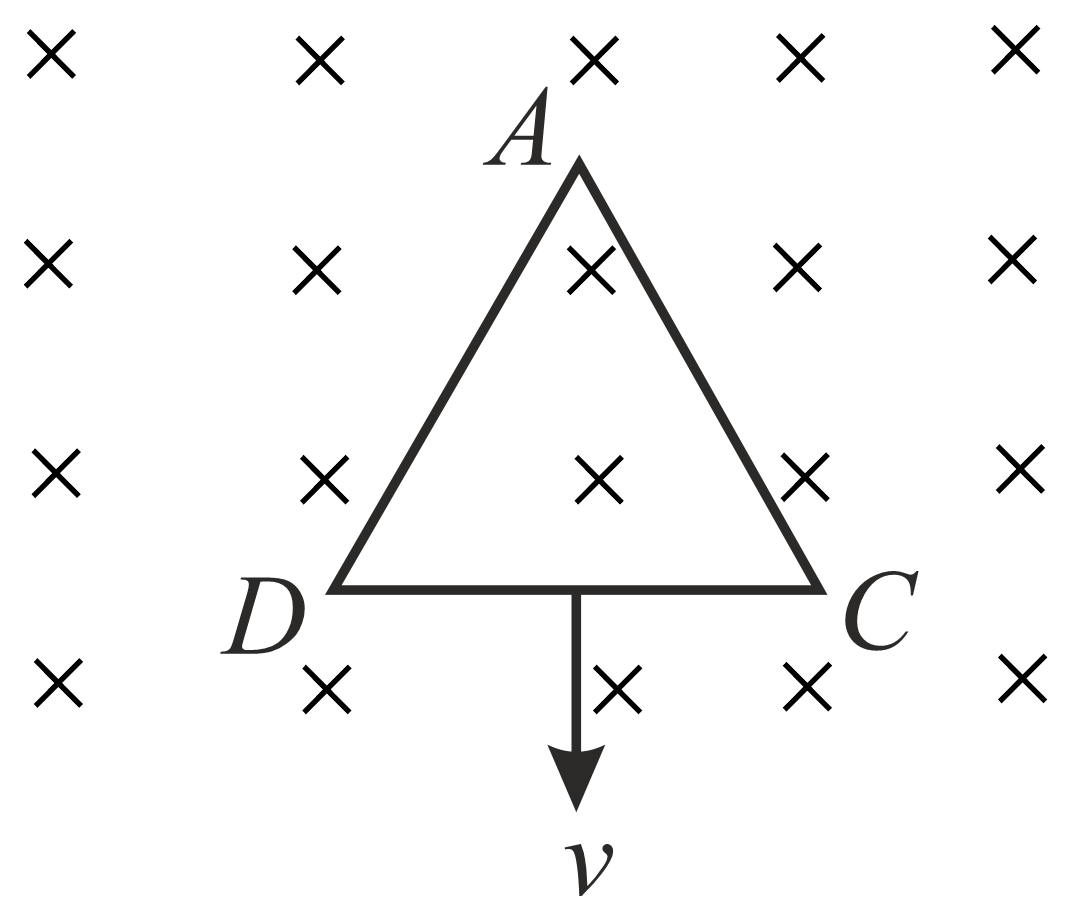
NTA AbhyasNTA Abhyas 2022
Solution:
