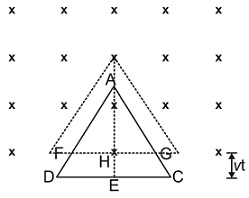
Question

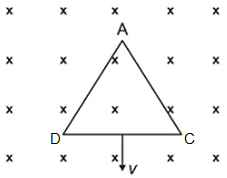
An equilateral triangular loop $ADC$ having some resistance is pulled with a constant velocity $v$ out of a uniform magnetic field directed into the screen. At time $t=0$ , side $DC$ of the loop is at edge of the magnetic field. The induced current $\left(i\right)$ versus time $\left(t\right)$ graph will be as

• A.
• B.
• C.
• D.

Answer 1

Answer: (B)

Let 2a be the side of the triangle and b the length AE.



$\frac{\text{AH}}{\text{AE}} = \frac{\text{GH}}{\text{EC}}$
$∴ \, \, \, \text{GH} = \left(\frac{\text{AH}}{\text{AE}}\right) \text{EC}$
or $\text{GH} = \frac{\left(\text{b} - \text{vt}\right)}{\text{b}} \cdot \text{a}$
$= \text{a} - \left(\frac{\text{a}}{\text{b}} \text{vt}\right)$
$∴ \, \, \, \text{FG} = 2 \text{GH} = 2 \left[\text{a} - \frac{\text{a}}{\text{b}} \text{vt}\right]$
Induced emf $\text{e} = \text{Bv} \left(\text{FG}\right) = 2 \text{Bv} \left(\text{a} - \frac{\text{a}}{\text{b}} \text{vt}\right)$
$∴ \, \, \, $ Induced current $\text{i} = \frac{\text{e}}{\text{R}} = \frac{2 \text{Bv}}{\text{R}} \left[\text{a} - \frac{\text{a}}{\text{b}} \text{vt}\right]$
or i = k₁ - k₂t
Thus, i-t graph is a straight line with negative slope and positive intercept.