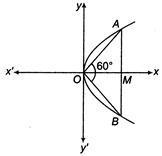
Q. An equilateral triangle is inscribed in the parabola $ {{y}^{2}}=4x $ . If a vertex of the triangle is at the vertex of the parabola, then the length of side of the triangle is
KEAMKEAM 2011
Solution:
Let $ OA=l, $ given, $ {{y}^{2}}=4x $ ...(i)
In $ \Delta OAM $ $ \sin 30{}^\circ =\frac{AM}{l}=\frac{1}{2} $
$ \Rightarrow $ $ AM=\frac{l}{2} $ and $ \cos 30{}^\circ =\frac{OM}{l}=\frac{\sqrt{3}}{2}\Rightarrow OM=\frac{l\sqrt{3}}{2} $ The coordinate of $ A=(OM,AM)=\left( \frac{l\sqrt{3}}{2},\frac{l}{2} \right) $ which satisfy the equation of parabola Eq. (i), $ {{\left( \frac{l}{2} \right)}^{2}}=4\left( \frac{l}{2} \right)\sqrt{3} $
$ \Rightarrow $ $ \frac{{{l}^{2}}}{4}=\frac{4l\sqrt{3}}{2} $
$ \Rightarrow $ $ l=8\sqrt{3}=OA $ Which is the required length of equilateral triangle.